Back to: Let’s Talk About Base Curves (Sample Lesson)
I cover base curve theory here because poor lens power (Rx) – frame matching is one of the most common problems in finishing. That relationship is covered in the lesson, Rx & Frame Matching in course #3: All About Frames.
Remember:
A high minus lens will have little or even no base curve and will work best in a frame with little or no curve.
A high plus lens will have a steep base curve and work best in a frame with some curvature.
Of course you will have customers that want their -4.50 in a heavily wrapped, fancy, sport-fishing sunglass!
A modern edger with the right grinding wheels (or router bits), good design software operated by an experienced user can overcome many, but not all, of the problems that poor Rx – Frame matching can create.
Here is a video series on understanding toric transposition or the relationship between the curves found on an eyeglass lens:
In optical theory it is said that the base curve is, “The curve from which all other curves are measured.”
In lens design we can think of the base curve as always being the front surface of the lens, D1 in the illustration.
In lens design that curve is always plus (+) and has a convex shape.
The corresponding curves that create the actual lens power (redirect light) are placed on the back of the lens, are minus (-) and have a concave shape, D2 in the illustration.
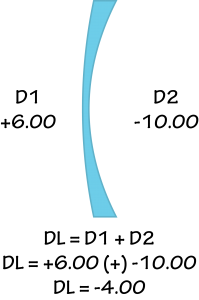
That relationship was covered in the lesson, The Nominal Lens Formula in the very first course, Optics For Opticians
Matching a base curve to create the wanted lens power is part of surfacing. Surfacing is the actual grinding away of the plastic on a lens to create the curves necessary to create power. These days surfacing is done at the “lab” not at the “store” and is no longer part of the day-to-day work of an optician.
Here is what I want you to know about base curve for your actual day-to-day work.
1) I want you to know that only a computer can determine the correct base curve on a lens designed using free-form technology. In fact most labs today will not allow you to change or request a base curve.
2) I want you to know that there are now lenses with variable base curve designs (the Camber series of progressive lenses from Younger). This means that the front base curve is actually fluid or variable or changing which further pushes base curve into theory over reality.
3) I want you to know that you will never attempt to change the lens base curve to match a frame base curve. You may hear some silly old fart or bad optician say, “Well, we will just run it on a ______ base instead.” Just smile, nod your head and then ignore them. Have the job finished at a good lab with a high-end edger. As I said, a good edger can overcome many (but not all) poor frame and Rx matching problems.
4) I want you to know that high-end sunglass makers like Costa, Rudy Project and Oakley are making a wide range of prescriptions in their wrap designs. This is done using some some special lens design but more through using sophisticated edgers. There are lenses designed to work better with wrap frames but that is about a different area of optics not about base curve or frame/lens finishing work.
Here is what you will need to know about base curve theory for the ABO or any practical exams you might need to take.
Again, these days this is just theory!
Both the methods below work off the spherical equivalent of the given prescription. The formula to determine the spherical equivalent of any Rx is:
Rx sphere power added to 1/2 the cylinder power. If the Rx is a sphere like -2.50 then you work with the -2.50. Spherical equivalents are also used in other formulas and when working with contact lenses.
The most basic rule is that you always want the base curve to be as close to +6.00 as you can get and still have the Rx work. In theory +6.00 should always give you the best possible combination of curves for weight, optics, etc.
Study the chart below. You will want to remember that the higher the plus power, the higher plus the base curve will become. The more minus the power (less plus power to minus power) the lower plus the base curve will become. A high minus Rx may even have a base curve of +0.25 or even 0.00.
To do that you can use Vogel’s Rule which is this:
For a plus prescription: Base Curve = Rx spherical equivalent + 6.00D
For a minus prescription: Base Curve = 1/2 the Rx spherical equivalent + 6.00D
Examples:
Choose the correct base curve for the following Rx: +4.50 -1.00 X 89
The spherical equivalent of that Rx is +4.00 [+4.50 (+) 1/2 of -1.00]
+4.00 (+) +6.00 = +10.00
Choose the correct base curve for the following Rx: -4.50 -1.00 X 89
The spherical equivalent of that Rx is -5.00 [-4.50 + 1/2 of -1.00]
1/2 of that spherical equivalent is -2.50 [-5.00/2]
-2.50 (+) +6.00 = +3.50
If your result is minus then you would go with 0.00 or plano.
-13.00 -3.00
-13.00 + half of cylinder = -14.50
-14.50 + 6.00 = -1.25
So plano or 0.00 front base curve.
Another common method is to simply use a base curve chart. Just make sure you are reading it correctly. You will find charts have overlapping ranges so you must be careful and be sure you are choosing the curve that is closest to that +6.00.
A simple base curve chart might look like this:
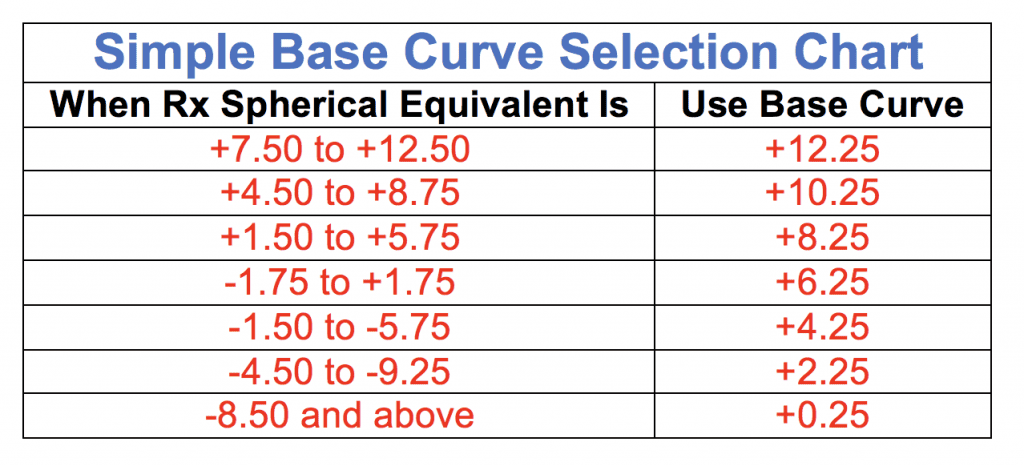
Examples:
Choose the correct base curve for the following Rx: +4.50 -1.00 X 89
The spherical equivalent of that Rx is +4.00 [+4.50 (+) 1/2 of -1.00]
+4.00 falls between +1.50 and +5.75 so our BC would be +8.25
Choose the correct base curve for the following Rx: -4.50 -1.00 X 89
The spherical equivalent of that Rx is -5.00 [-4.50 + 1/2 of -1.00]
-5.00 falls between -4.50 and -9.25
BUT it also falls between -1.50 and -5.75 and that BC is closer to our +6.00 so we choose +4.25 NOT +2.25.
