Back to: Vertex Distance
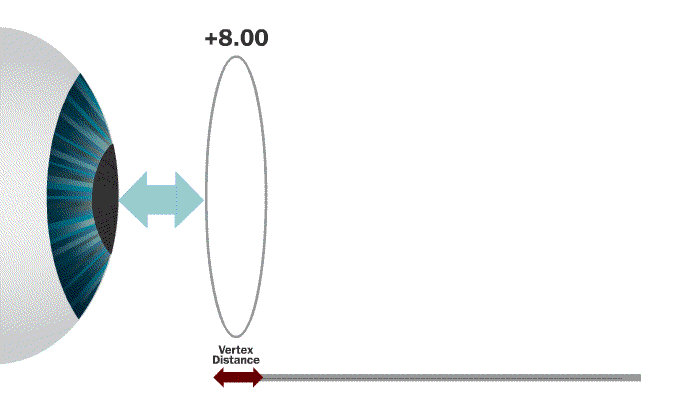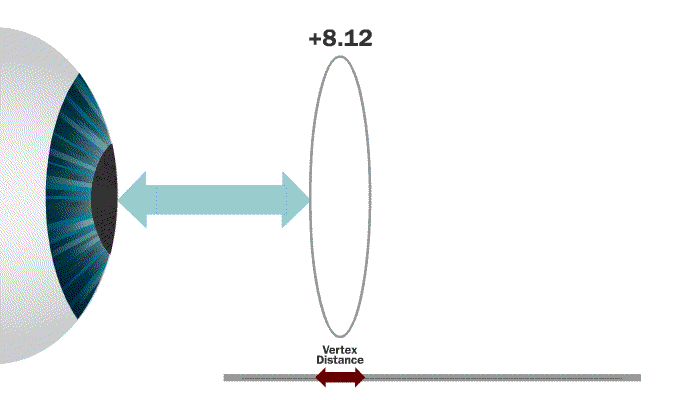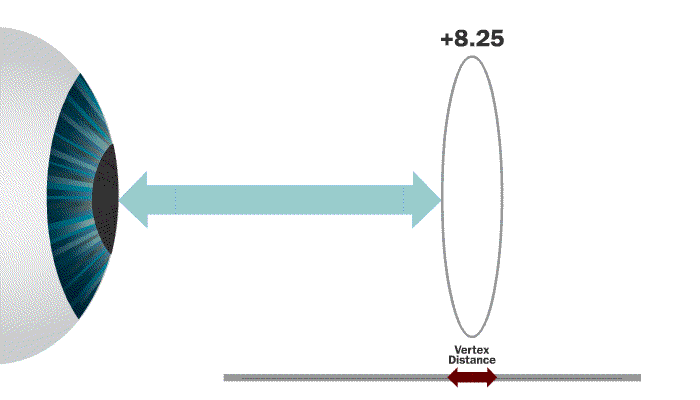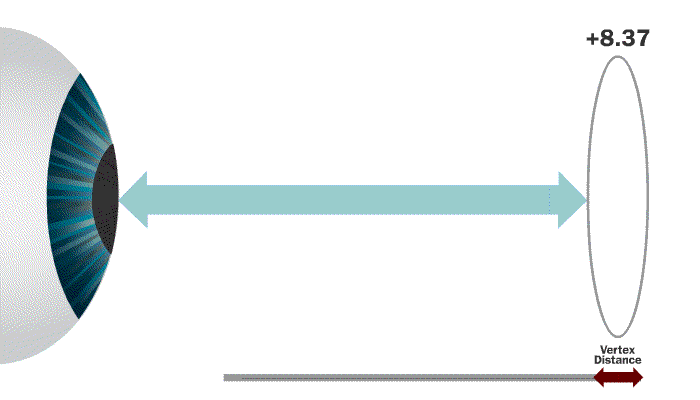
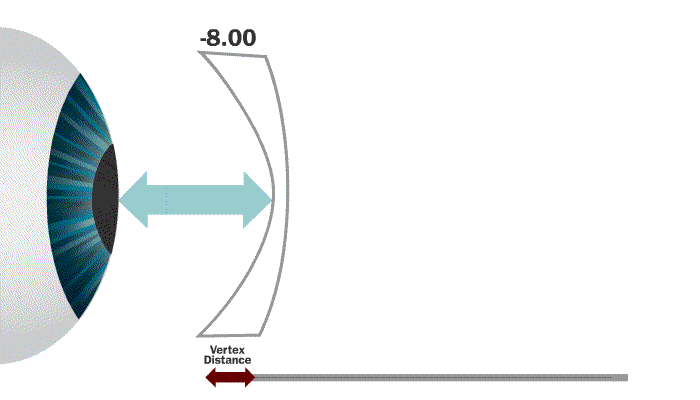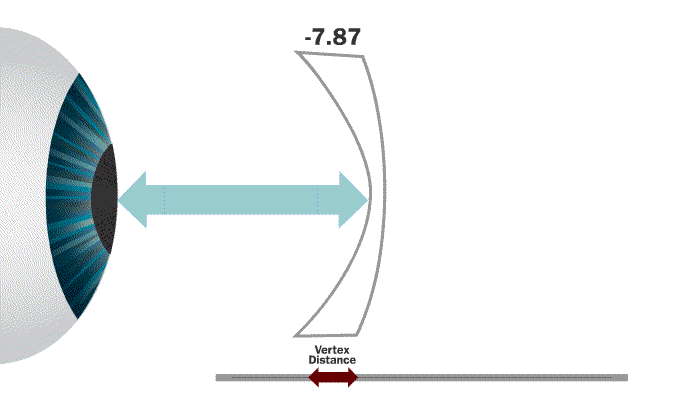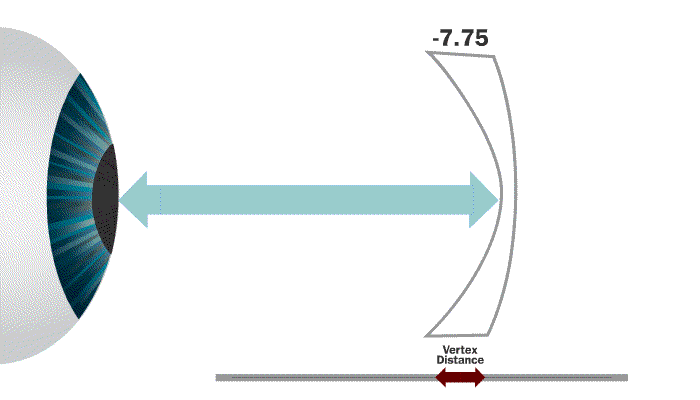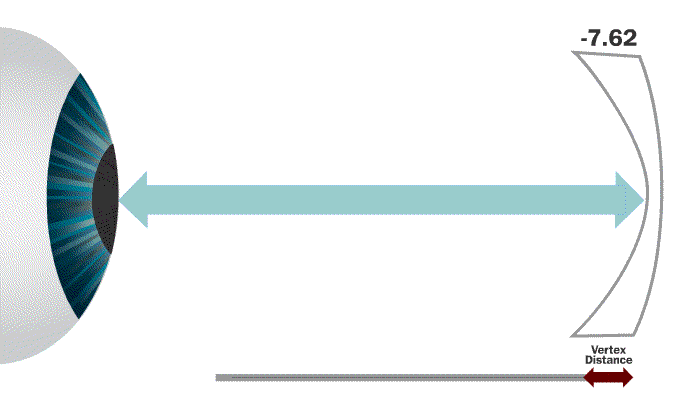
Vertex distance is the distance from the front surface of the cornea to the back side of a lens that is mounted in a frame and being worn by the patient.
The eye is actually a series of lenses that make up a focusing system. Because the eye is a self-focusing system, lenses placed in front of it will be perceived as having more or less strength depending on the distance they are set from the eye.
Note: The vision through the lens will be perceived by the brain as having more or less power. The actual power of the lens does not change.
This is as good a time as any to remember that “close-is-good” – you always want a lens to sit as close to the wearer as possible.
Why does vertex distance matter?
1) It explains why the prescription for contact lenses and glasses are often different
2) It can explain why a high-power prescription can be perceived as being “off” by a customer even when it is actually filled 100% correctly (*sort of)
3) Because you must know how to do these calculations to work with contact lenses
4) Because you must grasp the concept to pass your license exams
5)*Because vertex distance is a part of modern compensated prescriptions. If an Rx should call for +12.50 that perfect +12.50 is only perceived by the wearer when the glasses are worn at the same vertex distance as the phoropter or refraction device used to determine that need. Part of free form lens design is to provide the wearer with the perceived amount that is equal to what the Rx was actually written for.
Note: Free form lens design is calculated to the nearest 1/100th diopter not 1/4th.
Don’t worry more on all that later.
Did You Know: That just forty years ago patients who had cataract surgery did not receive an inter-ocular-lens (IOL) implant. These “aphakic” or literally “no lens” patients had no crystalline lens inside their eye. This meant that their eyeglasses had to compensate for all of the ‘plus power’ that was normally supplied by the crystalline lens. It was very common for prescriptions to reach +20.00D or beyond! These powers made it very important that eye care professionals knew how to compensate for vertex distance. Even the slightest difference between refracted and fit distances would make a dramatic difference for the patient. Thankfully, most patients now receive replacement lenses during cataract surgery and there is no longer a need for extremely hyperopic post-surgery prescriptions.
In the past the tool used most often to measure vertex distance is was the distometer:

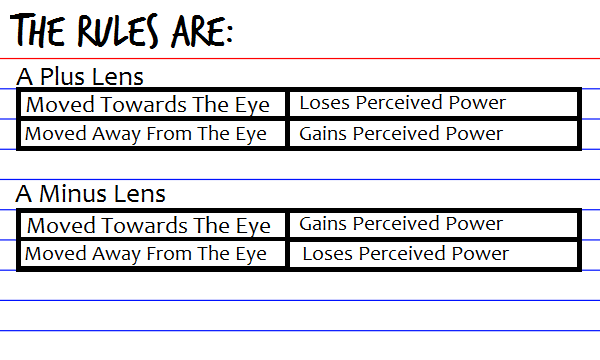
The most important thing to remember when understanding the concept of vertex distance is that in ALL circumstances, more vertex distance equates to more perceived plus power. LEARN THE RULES!
This is a good time to review a tricky concept:
“Less minus is more plus; less plus is more minus.”
-7.00 is “more plus” than -9.00. They are both minus powers, but -7.00 is “more plus” than -9.00.
+7.00 is more minus than +9.00 is. They are both plus powers, but +8.00 is “more minus” than +9.00.
How Does the Vertex Distance Calculation Work?
In this case we will figure out what the patient is perceiving in a pair that has already been made.
The formula is:
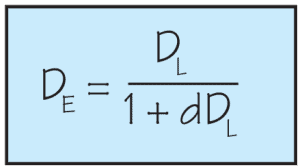
When:
DE is the power being perceived by the wearer.
DL is the actual power of the lens.
d is the distance between the where you want the lens and where it actually is.
If the lens is moved away from the eye you make d negative or add your minus sign
If the lens is moved closer to the eye you make d positive or leave it alone
Let’s say a customer brought you in a pair of glasses with the Rx of +18.00 OU.
The Rx was written with the lens in the phoropter placed 10mm away from the front of the cornea.
The customer wears the glasses at 15mm away from the front of his cornea.
A difference of 5mm further away.
Our rules above tell us that a + lens moved further away from the eye will increase in perceived power. This tells us that our result should be something above +18.00!
+18.00 / 1 (+) -0.005 X 18.00
-0.005 is 5 millimeters converted to meters which is what the formula is based on
It is -0.005 not 0.005 because the lens moved away from the eye (follow the rule above)
-0.005 X 18.00 = -0.09
1 (+) -0.09 = 0.91
18.00 / 0.91 = +19.78
This customer would perceive that their glasses were +1.78 diopters stronger than than they actually are.
To correct this the lenses would need to be remade at +16.22.
+18.00 – 1.78 = +16.22
We are NOT trying to correct them back to +18.00. We are trying to correct them, to wearing a lens that they perceive as it is worn, as providing them with +18.00. There is a difference between those two ideas. Their brain is already doing the adjustment on its own. Now we just need to make a lens that matches what their brain is seeing. If their brain is seeing the lens as being stronger we will lower the power. If their brain is seeing the lens as being weaker we would raise the power. That power, raised or lowered from what was actually written on the Rx is what we want. NOT to correct them back to the original amount written on the Rx. I know, I know, confusing to say the least. Just keep in mind that the brain is already doing the compensation and we are working from there.
Spherical Example 1
Let’s try another one using that +12.50 from above. In this case we will think ahead and provide the lab with enough information that they can make the lenses to the correct power as perceived by the wearer.
A person sits at an auto-refraction device and it determines that person needs +12.50 OU to see clearly. The device is set to a default vertex distance of 10mm. The customer is now in your store and chooses a frame. You measure that frame and find it sits just 8mm away from his eye.
You fill out the job order form for a modern free form lens and note, “Vertex distance 8mm – refracted at 10mm”
You have a difference in the as worn position of 2mm or the lens sitting 0.002 meters closer to the eye.
Our rule tells us that a + lens moved closer to the eye will lose perceived power. That tells us that our answer should be less than our +12.50.
+12.50 / 1 + 0.002 X 12.50
-0.002 is 2 millimeters converted to meters which is what the formula is based on
It is 0.002 not -0.002 because the lens moved closer to the eye (follow the rule above)
0.002 X 12.50 = 0.025
1 + 0.025 = 1.025
12.50 / 1.025 = 12.19 which is in fact a little weaker than our 12.50.
In a compensated lens design the lens would actually be made at +12.19 so the wearer perceived +12.50 in the as worn position.
Whew! I know, I know, a lot to get your arms around. Give it time…
Spherical Example 2
OK, one more with minus power this time.
Again to avoid a costly remake in this case we will think ahead and provide the lab with enough information that they can make the lenses to the correct power as perceived by the wearer.
A person sits at an auto-refraction device and it determines that a person needs -8.75 OU to see clearly. This device is set to a default vertex distance of 12mm. The customer is now in your store and chooses a frame. You measure that frame and find it sits 15mm away from his eye.
You fill out the job order form for a modern free form lens and note, “Vertex distance 15mm – refracted at 12mm”
You have a difference in the as worn position of 3mm or 0.003 meters further from the eye.
Our rule tells us that a minus lens moved further from the eye will lose perceived power. That tells us that our answer should be less than our -8.75.
-8.75 / 1 (+) -0.003 X -8.75
-0.003 is 3 millimeters converted to meters which is what the formula is based on
It is -0.003 not 0.003 because the lens moved further away from the eye (follow the rule above)
-0.003 X -8.75 = 0.026
1 + 0.026 = 1.026
-8.75 / 1.026 = -8.53 which is in fact a little weaker than our -8.75.
In a compensated lens design the lens would actually be made at -8.53 so the wearer perceived -8.75 in the as worn position.
It is OK if your head just exploded. It will become clearer with time and experience.
Sphero-Cylinder Example
A patient is prescribed: +18.00 -2.00 x 045 with the refraction instrument placed at 12mm away from the front of their cornea.
The glasses they chose (online) and had filled are worn at 9mm away.
We have a difference of 0.003 meters closer to the eye.
Because this is a sphero-cylinder lens we will need recalculate the entire Rx.
For our primary meridian of 45:
18.00 / 1 + 0.003 X 18.00
18.00 / 1 + 0.05
18.00 / 1.05 = 17.14
Or a perceived power 0.86 weaker which makes sense since this is a plus lens being moved closer to the eye.
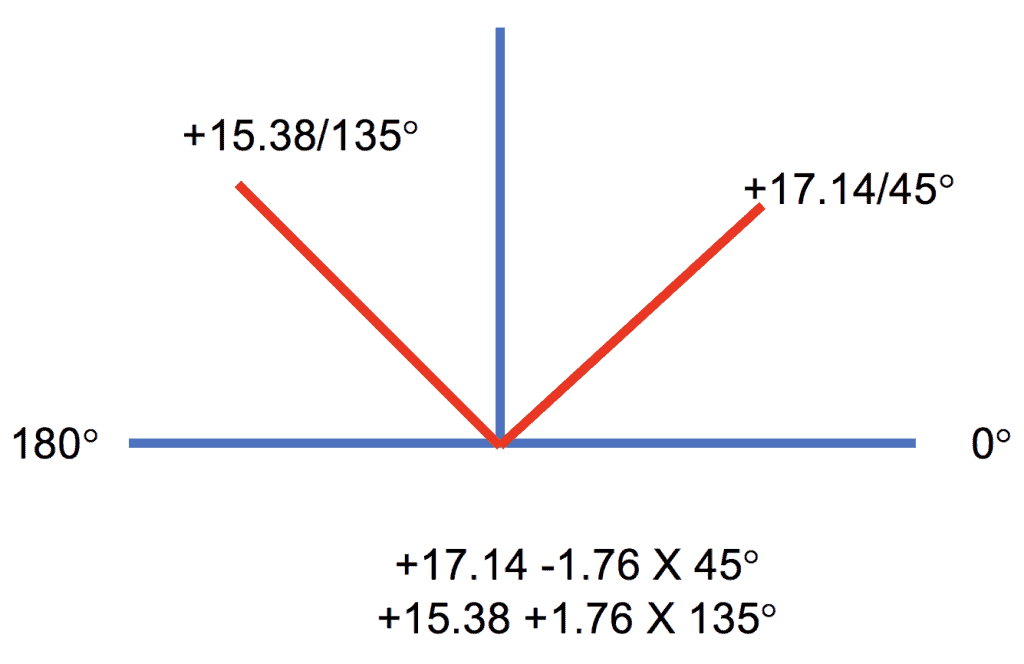
For our primary meridian 90 degrees away from 45 at 135:
Using flat transposition we find +16.00 at 135.
16.00 / 1 + 0.003 X 16.00
16.00 / 1 + 0.04
16.00 / 1.04 = 15.38
Or a perceived power 0.62 weaker which makes sense since this is a plus lens being moved closer to the eye.
If we toss these on an optical cross it would look like this:
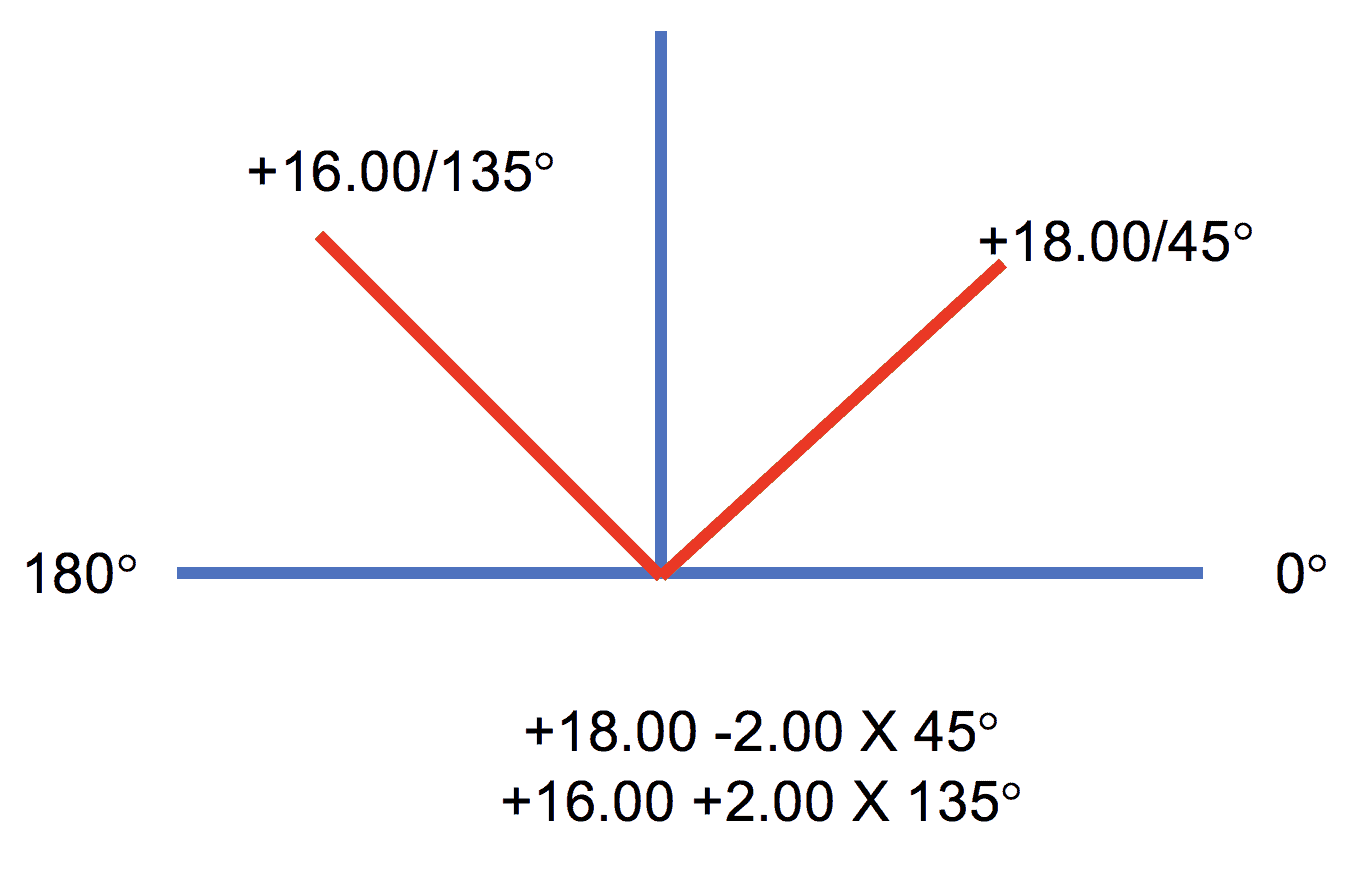
Vertex Distance & Contact Lenses
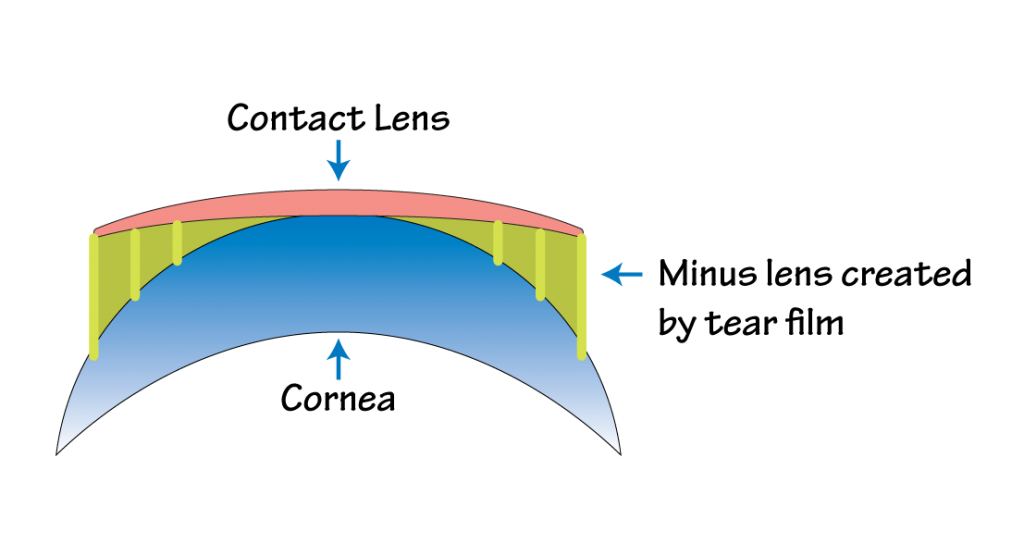
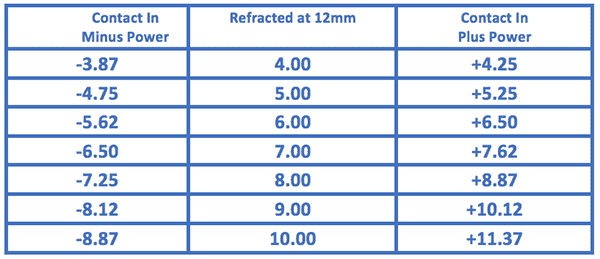
Since contact lenses are fit right on top of the cornea they are worn with virtually NO VERTEX DISTANCE. This can prove problematic; however, because most customers are refracted at a 10 to 14 mm distance. Due to the fact that there is such a great distance between refraction and fit for contact lenses all contact lens prescription over + or – 4.00 diopters need to be compensated for vertex distance. The chart below demonstrates the importance of vertex distance compensation while fitting contact lenses. Since compensating for vertex distance with contact lenses is so common, most practitioners will have a chart available that they can use for handy reference. It saves a lot of time – and paper.
I have no idea why I find this so fascinating but I do so here you go. The main reason that contact lens powers are different is that contact lenses create their own minus lens through your tear film! How cool is that?